
Then, we use the basic proportionality theorem to state the relationship between the sides of the triangle drawn. To prove the angle bisector theorem, we need to extend the sides of the triangle and make another triangle right next to it.

This is the statement of angle bisector theorem converse. If a line or a ray AD is drawn in ΔABC such that BD/DC = AB/AC, then AD bisects the ∠A. What is the Converse of the Angle Bisector Theorem? Write the converse of the statement, 'If something is a watermelon, then it has seeds.' We want to switch the hypothesis and the conclusion, which will give us: 'If something has seeds, then it is a watermelon.' Of course, this converse is obviously false, since apples, cucumbers, and sunflowers all have seeds and are not. It establishes a relation between the sides. The triangle angle bisector theorem can be used to find the missing lengths of the sides of a triangle.
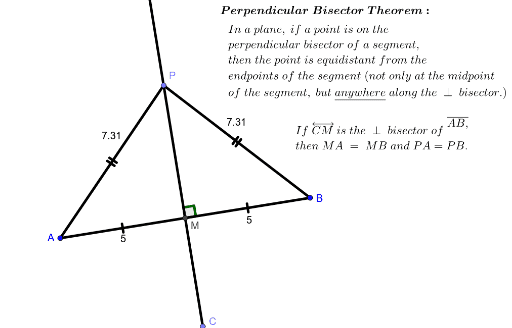
The only similarity between the side-splitter theorem and the angle bisector theorem is that both the theorems are related to the proportions of side lengths of the triangle. How are the Side-Splitter Theorem and the Angle Bisector Theorem Similar? This up-to-date treatment of recent developments in geometric inverse problems introduces graduate students and researchers to an exciting area of research. According to the angle bisector theorem formula, BD/DC = AB/AC. The triangle angle bisector theorem states that "The bisector of any angle inside a triangle divides the opposite side into two parts proportional to the other two sides of the triangle which contain the angle." What is the Formula for Angle Bisector Theorem? Since sides opposite to equal angles are equal, we have AC = AE.įAQs on Angle Bisector Theorem What is the Triangle Angle Bisector Theorem? Since AD is the bisector of ∠BAC, we have ∠DAB = ∠DAC - (4).įrom (2), (3), and (4), we can say that ∠CEA = ∠ACE. ∠DAC = ∠ACE ( alternate interior angles) - (3) The resulting theorems are powerful tools you can use to solve many real-world problems. These can be measured, compared, and transformed, and their properties and relationships can be proven using logical deduction.

We will be using the properties of the isosceles triangle to prove the converse as discussed below. Geometry involves the construction of points, lines, polygons, and three dimensional figures. This is exactly the reverse of the theorem we discussed above. ∠DAB = ∠CEA ( corresponding angles) - (2) The converse of isosceles triangle theorem states that if two angles of a triangle are congruent, then the sides opposite to the congruent angles are equal. Let's mark the angles in the above figure. Now, we are left with proving that AE = AC. Let us see the proof of this.ĭraw a ray CX parallel to AD, and extend BA to intersect this ray at E.īy the basic proportionality theorem, we have that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. Statement: In a triangle, the angle bisector of any angle will divide the opposite side in the ratio of the sides containing the angle.


 0 kommentar(er)
0 kommentar(er)
